Note: This is an old treatment. The early section on the Fine Structure Constant might be of interest. The rest not so much.
The Electron as Orbiting Quantum
by Ted R. King, Jr.
Abstract
Some implications of viewing the electron as an orbiting quantum are pursued to reveal interesting visualizations of electron spin, the Compton Wavelength, the Fine Structure Constant, the Heisenberg Uncertainty Principle, and possibly Schrödinger’s Equation. The Helix Wave Function describing the absolute path of the quantum is derived and explored for the non-relativistic case, and for the relativistic case of a constant velocity free electron. A full relativistic treatment is begun and carried to the first time derivative. The second derivative remains unexplored as yet.
The Electron as Orbiting Quantum
by Ted R. King, Jr.
1. The Isolated Electron at Rest
Viewing an isolated electron (or any particle) at rest as an orbiting
quantum:
The total relativistic energy E is the electron rest mass energy, and the equivalent
quantum energy is hf where h is Plank’s constant and f is the de Broglie
frequency of the electron. If c is the velocity of light, then from Special
Relativity and elementary quantum mechanics:
![]() (1.1)
(1.1)
the corresponding wavelength
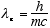 [2.43e-10
cm] (1.2)
[2.43e-10
cm] (1.2)
is the Compton wavelength of the electron.
1.1 Spin
If we specify the orbit, which we identify as the electron’s spin orbit,
as circular with a circumference of one wavelength, λe, then the
spin radius is
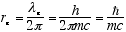 [3.86e-11 cm] (1.3)
[3.86e-11 cm] (1.3)
and the magnitude of the spin angular momentum is
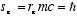 (1.4)
(1.4)
1.2 The Fine Structure Constant
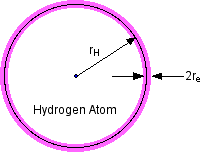
figure 1
The Bohr radius for the Hydrogen ground state is
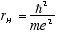 [5.3e-9
cm] (1.5)
[5.3e-9
cm] (1.5)
where e is the electron charge. The ratio
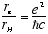 [1/137] (1.6)
[1/137] (1.6)
is the Fine Structure Constant.
An interesting physical correspondence I have not seen elsewhere.
2. The Free Electron
Consider an electron moving in the z direction at constant velocity, vz. For simplicity we assume it to be oriented with its angular momentum in the z direction as well so the orbiting quantum follows a helical path as shown in fig. 2. If it can indeed be in any random orientation, then its exact position and momentum will be uncertain :-)
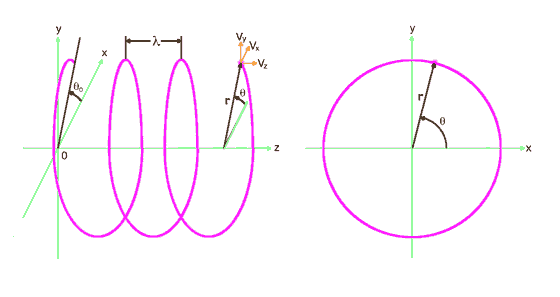
figure 2
For constant 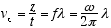
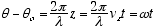 (2.1)
(2.1)
and 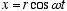
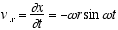 (2.2)
(2.2)

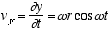 (2.3)
(2.3)
Since a quantum’s velocity is always c, we have
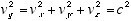 (2.4)
(2.4)
from which:
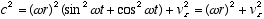
and 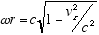 (2.5)
(2.5)
The de Broglie postulate E = hf specifies E as the total relativistic energy
of the particle, which in the observer frame is
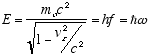 (2.6)
(2.6)
so 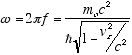 (2.7)
(2.7)
and from (2.5)
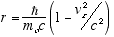 (2.8)
(2.8)
We see that r = |r| decreases with vz, which is to be expected
since E = hf means higher energies correspond to shorter wavelengths and thus
to smaller r. Interestingly, as vz approaches c, r approaches 0 and
the helix approaches the straight line path of a quantum with infinite energy.
3. Schrödinger’s Equation Revisited
Einstein postulated the quantization of em radiation in the photoelectric
effect by assuming the energy content E, of a quantum of energy of frequency
f is
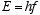 (3.1)
(3.1)
where h is Plank’s constant.
The wavelength of the radiation is obtained by the usual relation between its
wavelength λ, f, and v, the propagation velocity of the wave. This is
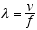 (3.2)
(3.2)
For em radiation v = c, the velocity of light, so
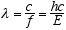 (3.3)
(3.3)
The quantum is characterized as a particle of zero rest mass, and total relativistic energy, E which is entirely kinetic. The general relation between total relativistic energy E, momentum, p, and rest mass, mo, is
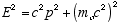 (3.4)
(3.4)
Since the rest mass of a quantum is zero we have for its momentum
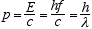 (3.5)
(3.5)
3.1 De Broglie’s Postulates
De Broglie figured if radiation waves could have a particle nature then maybe
particles could have a wave-like nature, and thus was born quantum mechanics.
He postulated that the wavelength, λ, and the frequency, f of the “pilot
waves” associated with a particle of momentum p and total relativistic
energy E are given by
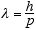
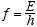 (3.6)
(3.6)
and that the motion of the particle is governed by the wave propagation properties
of the “pilot waves.”
3.2 Schrödinger’s Requirements
Schrödinger picked up from there searching for the corresponding propagation
equation. Changing de Broglie’s “pilot waves” terminology to
“wave function” to describe both the waves and the mathamatical function
Y(x,t), he adopted de Broglie’s postulates, but not de Broglies definition
of E as the total relativistic energy,
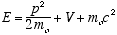 (3.7)
(3.7)
choosing instead the classical definition of total energy,
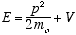 (3.8)
(3.8)
He then specified the following three requirements which the wave equation,
Y(x,t), must satisfy:
1. It must be consistent with the de Broglie postulates (3.6)
2. It must be linear in 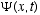 ,
i.e., if
,
i.e., if 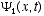 and
and 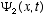 are solutions, then any linear combination of these
are solutions, then any linear combination of these 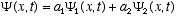 must also be a solution for any values of the constants
must also be a solution for any values of the constants 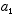 and
and 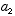 . This accomodates
superposition of waves to produce interference effects which we know occur.
. This accomodates
superposition of waves to produce interference effects which we know occur.
3. The potential energy V is, in general, a function of x and t. In the special
case 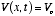 , a constant, the
momentum p and the energy E will also be constant. This is the situation of
a free particle moving at constant velocity for which it is required that the
wave equation have oscillatory traveling wave solutions of constant wave number
k = p/h and frequency f = E/h.
, a constant, the
momentum p and the energy E will also be constant. This is the situation of
a free particle moving at constant velocity for which it is required that the
wave equation have oscillatory traveling wave solutions of constant wave number
k = p/h and frequency f = E/h.
From these conditions Schrödinger derived his famous equation
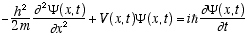 (3.9)
(3.9)
Solutions to Schrödinger’s equation for a free (constant velocity) particle
moving on the z axis are:
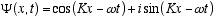 (3.10)
(3.10)
where k = 1/l = p/h = the wave number, and K = 2πk, and w = 2πf as given by
the de Broglie relations: f = E/h, and λ= h/p, where p is the particle momentum.
Y (z,t) is visualized as a traveling wave on the x axis with a real part and
an imaginary part which have previously been given only statistical significance
in calculating the probability of finding the particle at a coordinate x, i.e.,
not considered as pertaining to any physical reality on an individual particle
basis.
In fact, 3.10 also describes a traveling helical wave propagating in the x direction
normal to the complex plane.
4. The Helix Equation
From the treatment of section 2. of the postulated helical path of a
quantum which constitutes an electron, if we switch coordinate labels so Schrödinger’s
x is our z and our x and y become the complex plane, we write:
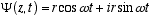 (4.1)
(4.1)
Which describes a quantum traveling at constant velocity vz on a
helical path around the z axis in terms of the complex plane coordinates. This
is not a solution to Schrödinger’s equation. Without the Kz term there
is no traveling wave, but what does it mean? Lets take a few derivatives and
see where it takes us.
The solution (4.1) to the helix equation can be written
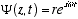
or in primed notation
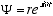 (4.2)
(4.2)
Taking time derivatives assuming vz and thus w and r constant
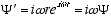 (4.3)
(4.3)
and 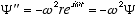 (4.5)
(4.5)
Defining 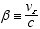 substituting
substituting
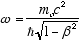 from (2.7) and
from (2.7) and
 from (2.8) gives
from (2.8) gives
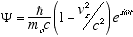 (4.6)
(4.6)
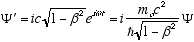 (4.7)
(4.7)
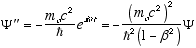 (4.8)
(4.8)
Multiplying both sides of (4.8) by the total relativistic energy
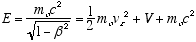 (4.9)
(4.9)
gives 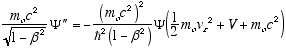
i.e. 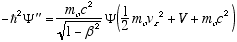
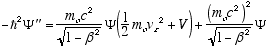
from (4.7) 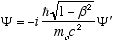
so 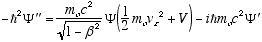
i.e. 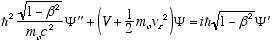
which in full notation gives
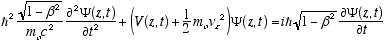 (4.10)
(4.10)
Which is the full relativistic equation for the helix model free particle (constant
vz). Of course in a non-zero potential V(z,t) vz is not
likely to be constant. The relativistic version of the helix equation for the
general case is derived in appendix A. Meanwhile, we continue with the non-relativistic
equation to see what happens in any potential V(z,t).
Unlike Schrödinger’s equation the second derivitive is a time derivative
instead of a space derivative. This is because there is no traveling wave.
Equation (4.10) is easily shown to satisfy requirements 1 and 2 of section 3.2,
but not 3 which requires a traveling helical wave when what we have is a traveling
particle on a helical wave trajectory.
Requirement 3 was based on the assumption that a particle is the more or less
localized wave packet resulting from the superposition of traveling waves. It
probably seemed the only way to account for the dual particle-wave nature of
reality. This seems no longer necessary.
In the general case with the potential energy V(z,t), vz = vz(z,t)
will not be constant.
4.1 The Non-Relativistic Helix Equation
For non-relativistic vz << c (4.10) becomes
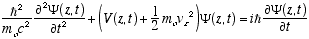 (4.11)
(4.11)The free particle solutions, Y(z,t) = reiwt can also be written (substituting from (2.6) and (2.8))
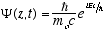 (4.12)
(4.12)Where
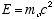
Note that unlike the Schrödinger equation, there is no space dependent part, Y(z,t) is just Y(t) in the non-relativistic free particle case.
4.1.1 Probability Not
Lets investigate the function
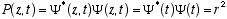
for the free particle case.
This is clearly not Born's probability function, but who needs it. We know where the damn particle is. It's just not always in the "real" plane, in fact it hardly ever is since it just passes through twice per cycle. We have been dealing all these years with the square of the projection of the r vector on the "real" plane, eliminating the bothersome "unreal" projection on the "imaginary" plane using the complex conjugate trick, and calling the result the probability of finding the "real" coordinate of the particle.
4.2 The Helix Wave Function in a General Potential V(z,t)
What happens to the solutions of (4.11) in the presence of a general potential V(z,t)? No longer is Y a function of time alone. The particle axis is no longer confined to the z axis. It can pull wheelies and backflips, and it can appear at the same space coordinates multiple times in the course of its travels given the appropriate potential field. But is its energy quantized? If it doesn't account for experimental emission and absorption lines and other observables as does the Standard Model, then this whole exercise illuminates a path going nowhere.
5. For Further Investigation
We have accounted for the mass of the electron as purely relativistic, and
its behavior, at least in inertial frames, with a visualizable model similar
to Schrödinger’s equation, but we have not addressed just what solution
to Maxwell’s equations, if any, describes such a circulating quantum which
exhibits conserved charge and a magnetic moment. It should also be very interesting
to explore the helical model in atomic settings and maybe make some animations
of what’s really happening when photons are emitted and absorbed, or during
pair production and annihilation. Maybe we will find new insight on other particles,
the nucleus, antimatter, gravity, and more. There is some reason why particle
masses and forces are what they are. Maybe with this visualization tool more
progress can be made.
Assuming all particle masses are similarly created, we should be able to express
all of physics in terms of momentum. There may be no such thing as mass.
Some Questions
How exactly does the momentum of one quantum interact with another?
Is the electron’s electric field truly spherical and constant? Have any
experiments verified this? Does every particle align its spin vector parallel
to the direction of travel? What about spin zero particles?
Does the helix model explain the two-slit experiment, Compton scattering, the
photoelectric effect, etc?
How does a proton capture an electron and become a Hydrogen atom? The corresponding
Compton wavelength and thus the radius of a proton is ~1/2000 that of the electron.
Does the electron bag the proton in its field as it passes through and get zapped
back and forth like the lasso of a lasso expert jumping back and forth through
his lasso? And if the proton doesn’t hit dead center, do the resulting
asymmetric ringing contortions look like the beautiful quantum states we have
plotted for the various H energy levels?
Are the quarks in a proton three quanta following bizarre paths that forbid
separation, or maybe just one following a really bizarre path, or maybe its
the same thing. More likely, the Maxwellian dynamics in atomic and nuclear domains
leave the simple helical path we have envisioned for the free electron (which
may itself be simplistic) behind for more complex geometries and dynamics. The
quantum may not need to be a particle at all.
What does the relativistic helix equation look like? This configuration begs
us to find out.
Appedix A - Derivation of the Relativistic Helix Equation
A1 Rules and Substitutions
For clarity the following differentiation rules and substitutions are posted
and numbered here for reference later:
Rules
1 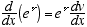 2
2
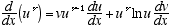
3 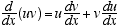
Substitutions
4 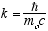 5
5 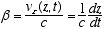
6 ![]() (2.7) 7
(2.7) 7
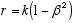 (2.8)
(2.8)
8 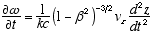 9
9 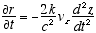
10 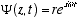 (4.2)
(4.2)
A2 Derivatives
10,3 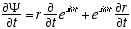 (A2.1)
(A2.1)
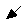

1 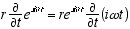 9
9
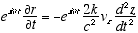
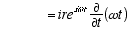 10
10
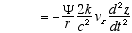
3 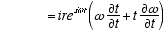
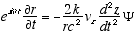 (A2.2)
(A2.2)
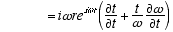
8,10 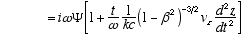
6 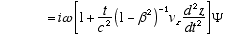
7 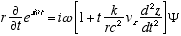 (A2.3)
(A2.3)
Combining (A2.3) and (A2.2)
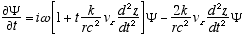
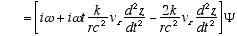
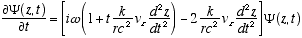 (A2.4)
(A2.4)
Which reduces to (4.3) for constant vz or vz << c. Remember
in (A2.4) that r and w are no longer constant, but functions of vz
as per (2.7) and (2.8). Thus (A2.4) really means
6,7 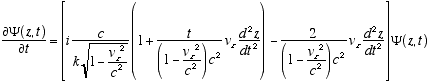 (A2.5)
(A2.5)
On to the second derivative:


